Verdiepingsstof HST 4 nsk-1
Brekingsindex
Een lichtstraal kan van richting veranderen wanneer hij overgaat in een andere stof. In het algemeen gelden de volgende twee regels:
- Een lichtstraal buigt naar de normaal toe wanneer hij overgaat van lucht naar een doorzichtige stof.
- Een lichtstraal buigt van de normaal af wanneer hij overgaat van een doorzichtige stof naar lucht.
De mate waarin hij afbuigt hang af van de Ďbrekingsindexí. Dit getal (zonder eenheid) geef de mogelijkheid om de hoek van breking (of de hoek van inval) te berekenen. De brekingsindex van veel stoffen is bekend. Zie daarvoor tabel 1
|
Stof |
Brekingsindex (geel licht) |
|
water |
1.333 |
|
diamant |
2.417 |
|
kwarts |
1.55 |
|
ijs |
1.309 |
|
aceton |
1.359 |
|
alcohol |
1.362 |
|
parafine |
1.48 |
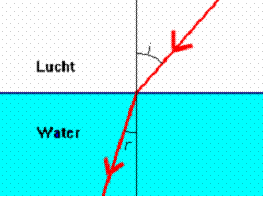
Figuur 1: breking bij
water
In figuur 1 is te zien hoe een lichtstraal overgaat van lucht naar water De hoek van inval (i) is hier 400 . De hoek van breking (r) is 18,70.
De hoek van inval is de hoek tussen de invallende lichtstraal en de normaal.
De hoek van breking is de hoek tussen de gebroken lichtstraal en de normaal.
Wanneer deze hoeken bekend zijn kan de brekingsindex bepaald worden met behulp van de volgende formule:
![]()
hierin is:
n = brekingsindex (zonder eenheid)
sin i = sinus van hoek van inval in graden
sin r = sinus van hoek van breking in graden.
In het geval van bovenstaande afbeelding wordt de
brekingsindex als volgt berekend:
![]()
De brekingsindex van de stof is dus 1.333. Deze stof is water want water heeft ook een brekingsindex van 1.333
Wanneer de brekingsindex bekend is kan hiermee bepaald worden hoe groot de hoek van breking zou zijn bij een bekende hoe van inval. Daarom het volgende voorbeeld:
Een lichtstraal van onder een hoek van 450† in op de stof diamand. Hoe groot is de hoek van breking?

Wanneer de brekingsindex bekend is kan hiermee berekend worden hoe groot de hoe van inval zou zijn bij een bekende hoek van breking. Daarom het volgende voorbeeld:
Een lichstraal valt op de stof parafine. De hoek van breking is 180. Bereken de
hoek van inval.
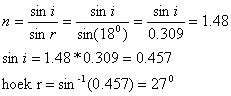
Lenssterkte
De sterkte van een lens kan berekend worden met:
![]()
Hierin is:
S = Lenssterkte in Dioptie (Dpt)
f = Brandpuntsafstand in m
Voorbeelden:
Een bolle lens heeft een brandpuntsafstand van 40 cm. Bereken de lenssterkte
Geg:
f = 40 cm = 0,4 m
![]()
Een brilleglas heeft een sterkte van -4 dpt. Bereken de brandpuntsafstand.
Geg:
S = -4 dpt
![]()
Wanneer er een voorwerp voor een willekeurige lens op een willekeurige afstand staat. Kunnen er twee soorten beelden ontstaan. Een virtueel beeld en een reŽel beeld. Een virtueel beeld is een beeld dat je niet op een scherm kunt opvangen. Een reŽel beeld kun je wel op een scherm opvangen. Daarbij zijn de volgende mogelijkheden:
Figuur 2 t/m 6: positieve lenzen.
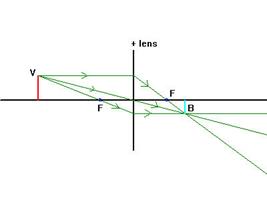
Figuur 2: v>2f; beeld is kleiner, omgekeerd, reeel
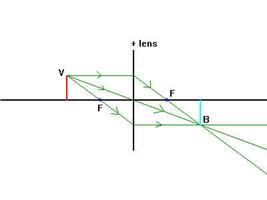
Figuur 3: v=2f; beeld is even groot, omgekeerd, reŽel
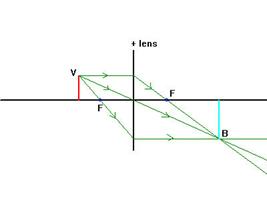
Figuur 4: 2f<v<f; beeld is groter, omgekeerd, reŽel
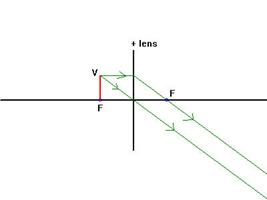
Figuur 5: v=f; geen snijpunten van lichtstralen, geen beeld
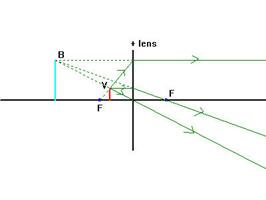
Figuur 6: v<f;
beeld is groter dan voorwerp, virtueel, rechtopstaand
Bij een holle lens ontstaat er altijd een virtueel beeld.
Dit beeld is teven altijd verkleind. In figuur 7 is daar een voorbeeld van te
zien. Wanneer de constructiestralen getekend worden, kruisen ze wel, alleen dan
aan de zelfde kant van de lens als waar het voorwerp staat.
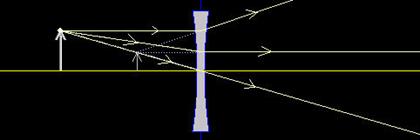
Figuur 7: bij een holle lens is het beeld altijd virtueel en verkleind.
lenzenformule
Er bestaand een verband tussen beeldafstand, voorwerpsafstand en brandpuntsafstand. Het boek omschrijft dit al volgt:
Wanneer de voorwerpsafstand groter wordt, wordt de beeldafstand kleiner.
Hoeveel kleiner is Ďkleinerí? Dit kan worden berekend met de lenzenformule. Dit is een formule die in de optica (Ďnatuurkunde die zich met verschijnselen van het licht bezighoudtí) die zeer veel gebruikt wordt en uiterst handig is voor diverse toepassingen.
![]()
Hier in is:
f = Brandpuntsafstand in m
v = voorwerpsafstand in m
b = beeldafstand in m
De volgende voorbeelden laten zien hoe deze formule werkt
VB 1:
Voor een positieve lens staat een voorwerp op een afstand van 0,5 m. De beeldafstand† van het scherpe beeld is 4 m. Bereken de brandpuntsafstand van de lens.
Geg:
v = 0,5 m
b = 4 m
![]() †
†
dus ![]()
om nu f uit te rekenen zal de omgekeerde waarde van 1/f berekend moeten worden
![]()
Wanneer de voorwerpsafstand of de beeldafstand berekend moet worden zal een eenvoudige aftreksommetje ingevoegd moeten worden. De volgende twee voorbeelden laten zien hoe dit in zijn werk gaat.
VB 2:
Voor een positieve lens (f = 20 cm) staat een voorwerp op een afstand van 40 cm. Bereken de beeldafstand.
Geg:
f = 20 cm = 0,2 m
v = 40 cm = 0,4 m
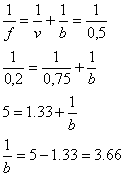
om nu b uit te rekenen zal de omgekeerde waarde van 1/b berekend moeten worden
![]()
VB 3:
Een diaprojector heeft een lens met een brandpuntsafstand van 15 cm. Het beeld staat op een afstand van 2,3 m van de lens. Op welke afstand zal de dia moeten staan?
Geg:
f = 15 cm = 0,15 m
b = 2,3 m
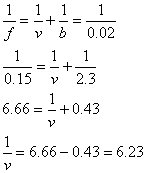
om nu b uit te rekenen zal de omgekeerde waarde van 1/b berekend moeten worden
![]()
Vergroting
In het boek staat dat de vergroting op de volgende wijze kan berekend worden:
![]()
Hierin is:
N = vergroting (zonder
eenheid!!)
B≠1B2 = Grootte beeld in m
V1V2 = Grootte voorwerp in m
De vergroting kan ook berekend worden met de volgende formule:
![]()
hierin is:
N = vergroting (zonder
eenheid!!)
b = beeldafstand in m
v = voorwerpsafstand in m
Voorbeelden:
In figuur 8 is een situatie te zien met daarin enkele gegevens. Bereken de grootte van het beeld. Het voorwerp is 2,3 cm hoog. De tekening is niet op schaal getekend. (met andere woorden: maak een berekening zonder in de tekening te meten met een geo o.i.d.)
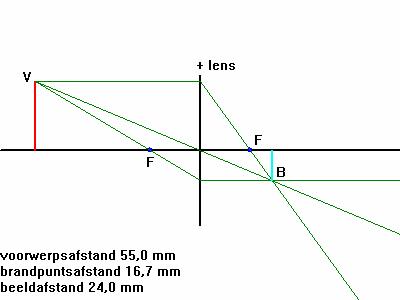
geg:
v = 55 mm = 0,055 m
b = 16,7 mm = 0,0167 m
f = 24 mm = 0,024 m
V1V2 = 2,6 cm = 0,023 m
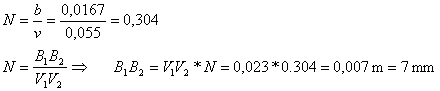
De grootte van het beeld is dus 7 mm